Positional game

Not to be confused with position or positional play in poker.

Positional games are a class of combinatorial games. Well-known games that fall into this class include tic-tac-toe, hex and Shannon switching game.

We say that 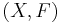$(X,F)$ is a positional game^[1], if $X$ is a finite set and $F$ is a collection of subsets of $X$ . We refer to $X$ as the board and $F$ as the winning sets. There are two players who alternately claim unclaimed elements of the board, until all the elements are claimed. Depending on the way the winner is determined, there are several versions of positional games.

Strong games

The player who is first to claim all elements of one winning set wins. If the game is over (all elements of the board are claimed) and no player has claimed all elements of a winning set, it is a draw.

Maker-Breaker games

The players are called Maker and Breaker. Maker wins if he claims all elements of one winning set. Breaker wins otherwise, i.e., he wins if the game is over (all elements of the board are claimed), and Maker did not claim a whole winning set. Note that a draw is not possible.

Avoider-enforcer games

The players are called Avoider and Enforcer. Enforcer wins if Avoider claims all elements of one winning set. Avoider wins otherwise, i.e., he wins if the game is over (all elements of the board are claimed), and he did not claim a whole winning set. Note that a draw is not possible.

References

^ J. Beck: Combinatorial Games: Tic-Tac-Toe Theory, Cambridge University Press, 2008.